By Raymond Reinhardt
Faculty Member, Mathematics at American Public University
What did the scarecrow say after being rewarded with his brains (actually, given a diploma) in “The Wizard of Oz”? And are there any practical applications for the Pythagorean Theorem?
His first brilliant remark was, “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.” You can watch this clip of the scarecrow yourself below.
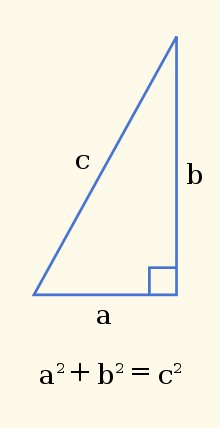
The scarecrow actually misquoted the theorem, but we can forgive his mistake, as the first full talkie movie came out in 1939, when few people had advanced mathematical background. I am confident that you have seen the correct formula in your high school algebra and geometry classes. The variables ‘a’ and ‘b’ represent the lengths of the legs, while the variable ‘c’ represents the length of the hypotenuse (longest side) of the right triangle.
So what good uses can we find for this well-known formula?
The Theorem can be applied to relationships that exhibit this exponent of two. The idea of “the length of a side” can be extended to fields other than pure mathematics.
- In computer science, for example, the theoretical time required for a bubble sort of n items requires a factor of n2 units of time. Similar to the Pythagorean Theorem, the time is the same for processing 130 items as for processing 50 items plus processing 120 items.
(130)2 = (50)2 + (120)2
This concept has led the bubble sort to be improved by using subgroups, as illustrated by the quick sort method.
Kalid, founder of BetterExplained.
Surprising Uses of the Pythagorean Theorem.
- In forensics, for example, investigators use the Pythagorean Theorem to determine bullet trajectory. Information such as how close the shooter was to the victim can ascertain whether the case is a homicide or suicide.
Ashley Seehow, eHow Contributor.
Real- Life Uses of the Pythagorean Theorem.
- At home, suppose you want to brag about how big your new TV is. You measure it to be 35 inches wide by 20 inches high. We can find the length of the diagonal by using Pythagoras’ theorem.
(35)2 + (20)2 =D2
1225 + 400 = D2
D = √1625 = approximately 40.3 inches diagonally
So we can brag about our new 40”- plus TV and invite the gang over for the playoffs or Superbowl.
I hope this has given you some insight into some practical uses of the famous formula, or at least the scarecrow’s attempt at the Pythagorean Theorem, as found in “The Wizard of Oz.”
About the Author
Raymond Reinhardt is an instructor of mathematics in the School of Science, Technology, Engineering and Mathematics at American Public University. He holds both a bachelor’s and a master’s degree in Mathematics. He has extensive teaching experience — having taught mathematics for over 44 years at the high school and college levels.
Comments are closed.